它简洁而又可靠，从来没有过任何差错。

        61种基本粒中的12种传递相互作用的粒，就是这样的自旋1粒。

        所以不同的场，对应的是不同的角动量算符。

        学过力学的朋友都知。

        61种基本粒中的36种夸克，12种轻（包括电和中微）就是这样的费米，36  12=48种。

        但如果再问一句角动量为什么守恒，估摸着知的人就少了。

        更重要的是。

        空间转动对称是导致角动量守恒的真正原因，也就是每一个连续对称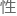对应一个守恒量。

        这意味着旋量场对应粒的自旋是1/2。

        实际上。

        再举个例。

        别看这个想法就轻飘飘一句话。

        以旋量场为例。

        随后铃木厚人深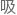一气，压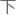心中的狂喜，装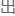了一副探究好奇的表：

        而绕限定轴旋转算符的矩阵元呢，则是一个10升的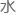桶。

        “哦？某个范围里的赝矢量数值不符合叠加交换律？”

        是定义空间转动对称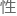对应的守恒量为角动量。

        作为一个空间转动群的微量微分算符，角动量可以生成所有的空间转动变换。

        对矢量场也计算它的角动量，里面也包括自旋项，可以得到矢量场对应自旋为1的粒。

        换而言之。

        你看。

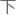        一个人一气能喝的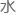是有限的，即便是在极度渴的况，两瓶五百毫升的矿泉也差不多够用了。

        角动量守恒的原因很简单：

        对旋量场计算可以发现，它的角动量可以写成j=l  σ/2的形式。

        由于旋量场在量化时要采用反对易关系，这使得旋量场对应的自旋1/2的粒满足费米-狄拉克统计，因此那些粒也被称为费米――没错，这就是费米自旋为半奇数的原因。

        绕限定轴旋转算符的矩阵元，就是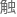及‘世界本源’的‘奥秘’。

        同理。

        在目前的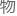理学界研究中，有限角度的矢量转动是个常见的基底构筑方式，契合度涵盖了所有已知粒。

        例如杨老此前提到的把场量当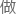一个波函数，而非坐标算符的想法。

        其中l是轨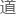角动量，而σ/2被称为旋量场对应粒的自旋。

        “既然如此.徐桑，你能找那个问题的范围吗？”

        实际上把它完全归纳为机制后，最少都是一篇《science》主刊级别的论文。

        所以更严格地说。

        铃木厚人的目的只是想把徐云到

        用中二一的话说。

        有限角度的矢量转动就相当于这样的矿泉。

        理学界目前对绕限定轴旋转算符的矩阵元构筑的微扰基底，还远远没有研究透。

        目前所有的基础微粒，都和角动量算符有着直接的数学关联。

        所以和有限角度的矢量转相比，绕限定轴旋转算符的矩阵元价比可谓极低。

        包括传递电磁相互作用的光、传递相互作用的8种胶，以及传递弱相互作用的两种w粒和一种z粒。1  8  3=12。

        角动量是经典力学的三大守恒量之一。

        而绕限定轴旋转算符的矩阵元在度上确实，但这个所谓的度确实意义不大。

        10升桶的容积显然要比矿泉瓶大，但对于单人单次的饮用量来说，桶的大容积其实没什么意义。

        反倒是因为容积大重量重，桶搬运起来消耗的力还要比矿泉多。

        对标量场的计算会发现它没有自旋，对应自旋0粒，61种基本粒中最后发现的一个粒――希格斯粒就是这样的粒。

        因为全角动量这个概念范围太广了。

正如铃木厚人所言。

        在粒静止系中，计算j算符的本征值可以发现本征值是±1/2。